Deep learning is essentially a deep artificial neural network, and it is not an isolated technology. Rather, it is the result of combining mathematics, statistical machine learning, computer science, and artificial neural networks. To truly understand deep learning, one must have a solid foundation in undergraduate-level mathematics, such as mathematical analysis, linear algebra, probability theory, and convex optimization. These subjects provide the theoretical backbone necessary for grasping the inner workings of neural networks.
Moreover, mastering deep learning requires hands-on practice with programming at its core. Without a strong background in both mathematics and computer science, any attempt to achieve breakthroughs in this field would be like building a house on sand. Therefore, beginners aiming to succeed in deep learning should first grasp the significance of these foundational concepts. Our professional path will explore deep learning from both theoretical and practical perspectives, analyzing advanced techniques through the use of deep learning frameworks.
Finally, we will share real-world experiences in applying deep learning and discuss how to stay updated with the latest research and trends in the field.
**Mathematical Foundation**
To fully understand the mathematical formulas in deep learning papers and even derive new methods independently, one must have a strong mathematical foundation. A good grasp of the four key courses—mathematical analysis, linear algebra, probability theory, and convex optimization—is essential. Additionally, familiarity with basic machine learning theories and algorithms is crucial for deeper understanding.
**Mathematical Analysis**
Calculus is the main focus in advanced mathematics, especially for deep learning applications. Key topics include functions, limits, derivatives (especially chain rule), integrals, power series, and differential equations. Understanding the derivative of a function is fundamental during the optimization process. Concepts like the mean value theorem, Taylor expansion, and Lagrange multipliers are also important. For further study, the 5th edition of *Advanced Mathematics* by Tongji University is highly recommended.
**Linear Algebra**
Linear algebra is central to deep learning due to its emphasis on vectors and matrices. It covers vector spaces, matrix operations, determinants, eigenvalues, and more. Being able to interpret Jacobian or Hessian matrices and manipulate loss functions in matrix form is critical. The 6th edition of *Linear Algebra* by Tongji University is a great resource.
**Probability Theory**
Probability theory is vital in deep learning, especially for understanding stochastic processes like stochastic gradient descent, parameter initialization (e.g., Xavier), and regularization techniques like Dropout. Mastery of random variables, distributions, laws of large numbers, and hypothesis testing is necessary. The *Probability Theory and Mathematical Statistics* textbook from Zhejiang University is a solid choice.
**Convex Optimization**
While convex optimization is an applied branch of mathematics, it plays a key role in understanding deep learning optimization. Familiarity with convex sets, functions, and basic optimization methods like gradient descent and Newton’s method is sufficient for most practitioners. *Convex Optimization* by Stephen Boyd is a recommended textbook.
**Machine Learning**
Deep learning is just one subset of machine learning. To excel, one must understand classical techniques like regression, SVMs, random forests, and model selection. Further knowledge in semi-supervised, unsupervised, and reinforcement learning is also beneficial. *The Elements of Statistical Learning* is a classic reference.
**Computer Basics**
Practical deep learning involves hardware, operating systems, and programming. Proficiency in Linux, shell scripting, and languages like C++ and Python is essential. Deep learning engineers often need to work across multiple layers, from high-level Python scripts to low-level C++ implementations.
**Programming Languages**
Python is widely used for prototyping and data processing, while C++ remains popular for performance-critical components. Frameworks like TensorFlow and PyTorch are built using C++, but Python is commonly used for model development. Recommended books include *C++ Primer* and *Python Core Programming*.
**Linux Operating System**
Most deep learning systems run on Linux. Familiarity with command-line tools, file systems, and text editors like VIM is crucial. *Bird's Linux Private Kitchen* is a useful guide.
**CUDA Programming**
GPU acceleration is essential for deep learning. NVIDIA’s CUDA toolkit allows developers to harness GPU power efficiently. The official documentation is a valuable resource.
**Other Computer Skills**
Beyond basic programming, knowledge of data structures, distributed computing, and hardware architecture (like PCIe) can greatly enhance one’s ability to optimize and debug deep learning models.
**Introduction to Deep Learning**
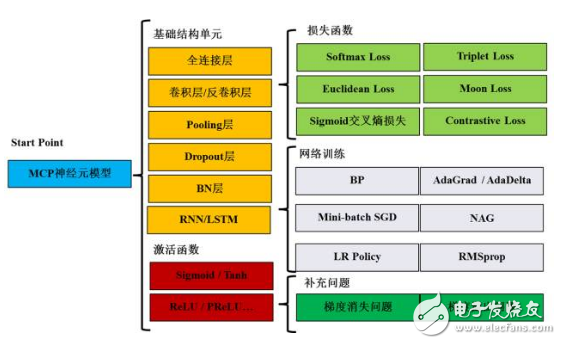
In the next section, we will introduce the theoretical foundations of deep learning, including neuron models, convolutional and pooling layers, activation functions, loss functions, and classical architectures like MLP and CNNs. We will also cover training methods such as backpropagation and SGD, and discuss challenges like vanishing and exploding gradients.
Copper Clad Ceramic Plate Series
Copper clad ceramic plate series
YANGZHOU POSITIONING TECH CO., LTD. , https://www.yzpst.com