Abstract: In view of the shortcomings of conventional feature extraction methods, a feature extraction method based on BP neural network and mutual information entropy is proposed, and an example of feature extraction is illustrated. The results show that these two methods are feasible and effective.
With the development of science and technology, the structure of modern equipment is becoming more and more complex, and there are more and more types of failures, which reflect the status and characteristics of the failures. In the actual fault diagnosis process, in order to make the diagnosis accurate and reliable, always collect as many samples as possible to obtain sufficient fault information. However, too many samples will occupy a lot of storage space and calculation time. Too many feature inputs will cause the training process to be time-consuming and labor-intensive, and even hinder the convergence of the training network, which ultimately affects the classification accuracy. Therefore, it is necessary to extract useful information that contributes greatly to the diagnosis of faults from the sample. This job is feature extraction.
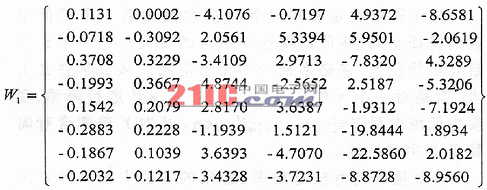
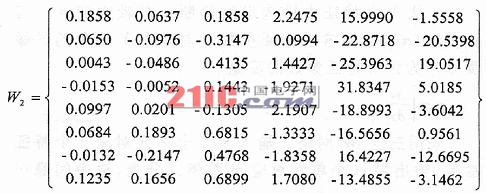
Feature extraction is to use the existing feature parameters to construct a lower dimensional feature space, map the useful information contained in the original features to a few features, and ignore the extraneous and irrelevant information. In a mathematical sense, it is to reduce the dimension of an n-dimensional vector X = [x1, x2, ..., xn] T, and transform into a low-dimensional vector Y = [y1, y2, ..., ym] T, m There are many methods for feature extraction. Commonly used methods are Euclidean distance method, probability distance method, statistical histogram method, divergence criterion method, etc. Aiming at the limitation of existing methods, this paper studies the feature extraction method based on BP neural network and the feature extraction method based on mutual information entropy. 1 Feature extraction method based on BP neural network It is necessary to select n feature parameters (n εij = | (аYi) / (аXj) | Using a three-layer BP network, n units in the input layer correspond to n feature parameters, m units in the output layer correspond to m kinds of pattern classification, the number of intermediate hidden layer units is q, and WB iq is used to denote the input layer unit i and hidden layer unit q The connection weight between the two; using w O qj to represent the connection weight between the hidden layer unit q and the output layer unit j, then the output Oq of the hidden layer unit q is: The output yj of the jth unit of the output layer is: Where j = 1, 2, ..., m; εj is the threshold. Then the sensitivity of the characteristic parameter xi to the model category yj is: Substituting into equation (1), the difference between the sensitivity εij of the characteristic parameter Xi and the sensitivity εkj of the characteristic parameter Xk can be sorted as: A large number of experiments and studies have shown that when the network converges: a1≈a2≈ ... ≈aq. As can be seen from the above formula, if: Then there must be: εij > εki That is, the characteristic parameter Xi is better than the characteristic parameter Xk in classifying the j-th fault. The sample set composed of the feature parameter X and the classification pattern classification result y is used as the learning sample of the BP network to train the network. Let Wiq and Wkq be the connection weight coefficients between the input unit and the hidden layer unit q corresponding to the characteristic parameters Xi and Xk, respectively: │Wεi│ = │Wi1│ + | Wi2 | +… + | Wiq | │Wεk│ = │Wk1│ + | Wk2 | +… + | Wkq | If │Wεi│> │Wεk│, it can be considered that the characteristic sensitivity εi of Xi is greater than the sensitivity εk of the characteristic parameter Xk. This shows that the classification capability of the feature parameter Xi is stronger than the classification capability of the feature parameter Xk. 2 Feature extraction method based on mutual information entropy It can be seen from the information characteristics that when a feature obtains the maximum mutual information entropy, the feature can obtain the maximum recognition entropy increment and the minimum false recognition probability, and thus has the optimal characteristics. The feature extraction process is to find a set with the largest mutual information entropy under the initial feature set consisting of the given n feature sets X2 {XI ~ X2, ..., zn): X = {X1, X2, …, Xk}, k Under a certain initial feature set, the posterior entropy of the identified samples is certain. In the process of implementing feature optimization, with the deletion of features, there will be loss of information, making the posterior entropy tend to increase. Therefore, the size of the posterior entropy increase reflects the situation of information loss caused by deleting feature vectors. When deleting different features and increasing the number of deleted features, there will be different posterior entropies. According to the posterior entropy from small to large, the corresponding feature deletion sequence can be obtained. The process can be described as: (1) Initialization: Let the original feature set F = {N features}, let the initial optimized feature set S = [K features, K = N]; (2) Calculate the posterior entropy; (3) Decreasing: S = [K-1 features], and calculate the corresponding posterior entropy; (4) Select the optimized feature set: based on the posterior entropy corresponding to multiple decreasing feature sets, select the feature vector set with the smallest posterior entropy increase as the optimized feature set S [N-1 optimized features]; (5) Return to (3), recalculate until the classification requirements are met, and select the optimal feature set with the smallest posterior entropy; (6) Output optimized feature set. 3 Examples of feature extraction In the work of generating sets of thermal power plants, the main shafts of generating sets often encounter failures such as surge and fluid excitation. These failures will not only cause a drop in production efficiency, but also cause serious harm to the machine and affect the safe operation of the unit. The traditional diagnosis method is to add a sensor at the spindle bearing to perform vibration test to obtain its spectrum; then analyze in the frequency domain, quantify the power spectrum density of the vibration signal according to certain rules according to the fault diagnosis theory based on energy distribution, and use a neural network And other tools for troubleshooting. However, faults such as surge and fluid excitation usually appear as continuously distributed colored noise bands in the frequency domain. Analysis in the frequency domain is difficult to distinguish, and it is difficult to extract spectral features. Holographic spectrum analysis methods are also not very effective. The traditional method increases the system overhead, and the diagnosis effect is not ideal. If the information optimization method is used for preprocessing in the time domain, and then the traditional diagnosis method is used for diagnosis, good results can be obtained. In this paper, the parameters such as variance, kurtosis, and skewness of the fault vibration signal in the time domain are used to extract features using BP neural network and posterior entropy analysis, and how to find the features that can best reflect the fault. Table 1 is the data of 6 parameters such as the variance, kurtosis, and skewness of the vibration signal in the vertical and horizontal directions when the main shaft surge and fluid excitation failure. Let the original feature set F = {x1, x2, x3, x4, x5, x6}, where x1 and x2 are the mean square deviations in the vertical and horizontal directions, x3 and x4 are the steepness in the vertical and horizontal directions, x5, x6, respectively , Respectively, the vertical and horizontal skewness. ①Feature extraction method based on BP neural network: the data in Table 1 is used as the input of BP neural network, and a program is prepared to train the neural network. The training algorithm uses standard BP algorithm and Levenberg-Mar-quardt method to train BP The network calculates the characteristic sensitivity of the characteristic parameters and determines the characteristic parameters that have the greatest impact on the results. Surge: │W1│ = {1.5874 1.6553 25.5320 25.1765 74.4724 40.4295} Fluid excitation: │W2│ = {1.5874 1.6553 25.5320 25.1765 74.4724 40.4295} It can be seen from the results that the skewness is the most sensitive to these two faults, reflecting the main characteristics of low-frequency self-excited faults. ② Feature extraction method based on mutual information entropy: The original feature set F = {x1, x2, x3, x4, x5, x6} corresponds to the feature parameters in Table 1. During the optimization of feature parameters, with the deletion of features, the posterior entropy changes greatly. When the deleted features include x5 and x6, the posterior entropy decreases significantly; if only x5 and x6 are retained, the posterior entropy is the smallest. It shows that the skewness is the most sensitive to these two faults. Comparing these two feature extraction methods, we can see that they have the same conclusion. If pass-through holographic spectroscopy is used for analysis, the same conclusion is obtained, thus verifying the effectiveness of these two feature extraction methods. In actual condition monitoring and fault diagnosis, you can focus on monitoring the skewness of the system, combined with spectrum analysis of the vibration signal, you can quickly determine the type of fault and the specific time of occurrence.
Terminal block is a kind of accessory product used to realize electrical connection, which is divided into connector category in industry. With the higher degree of industrial automation and the more strict and precise requirements of industrial control, the amount of terminal is increasing. With the development of electronic industry, more and more terminals are used, and there are more and more types.
So each part of the terminal block is very important. For example, hardware, there are all copper, copper, stainless steel and so on.
Terminal Blocks Independent Parts Brass Terminal Block,Brass Earth Terminal,Brass Connector Block,Waterproof Terminal Block Suzhou WeBest Electronics Technology Co.Ltd , https://www.webestet.com
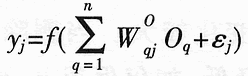
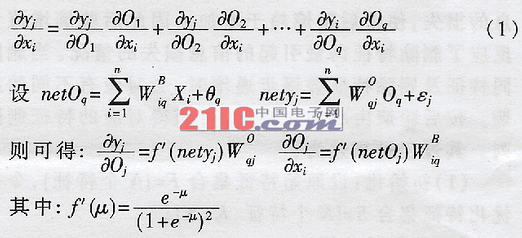


Table 1 Characteristic parameters of spindle failure Serial number Surge Fluid excitation Mean square error Steepness Skewness Mean square error Steepness Skewness vertical Level vertical Level vertical Level vertical Level vertical Level vertical Level 1 7.50 9.21 -0.02 -0.00 -0.22 -0.10 40.2 44.1 0.22 -0.42 -0.11 -0.08 2 26.1 15.2 -0.75 -0.92 -0.31 -0.21 70.1 20.5 3.82 1.78 0.00 0.16 3 13.8 9.21 -0.81 -0.72 -0.29 0.19 12.4 14.2 -0.38 -0.62 0.03 0.01 4 6.2 8.5 -0.01 -0.04 -0.22 -0.23 8.15 33.5 0.15 -0.14 0.07 0.10 5 36.1 11.2 -0.61 -0.01 -0.23 0.07 7.21 15.2 -0.41 -0.51 0.01 0.01 6 11.5 9.71 -0.81 -0.93 -0.31 -0.18 25.7 30.2 -0.37 0.19 -0.11 -0.06 7 33.1 28.2 -0.79 -0.85 -0.07 -0.45 71.2 25.3 3.81 1.85 0.01 0.16 8 37.2 26.8 -0.81 -0.87 -0.06 -0.41 8.11 35.2 -0.81 -0.13 0.01 0.11